자료구조와 알고리즘의 이해
data structure, algorithm, Big-O
알고리즘을 정리하고,
프로그래머스의 문제를 바탕으로 활용해보는 연재.
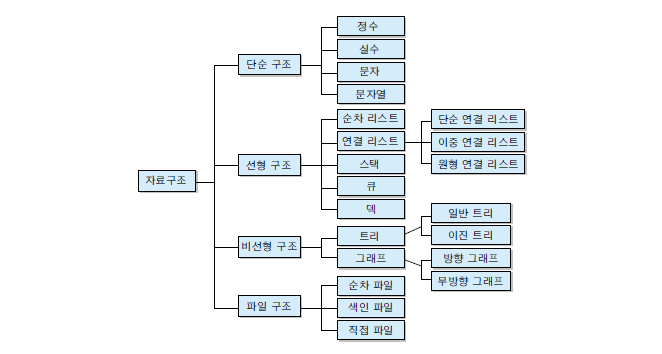
자료구조(Data Structure)
정의
- 데이터를 표현하고 저장하는 방법
분류
알고리즘(Algorithm)
정의
- 표현 및 저장된 데이터를 대상으로 하는 문제의 해결방법
- 자료구조가 결정되어야 그에 따른 효율적인 알고리즘을 결정할 수 있다
성능 분석
- 시간 복잡도(time complexity)
- 알고리즘의 수행
시간분석결과,속도에 해당 - 연산 횟수를 통해서 알고리즘의 빠르기를 판단
- 처리해야 할 데이터의 수 n에 대한 연산 횟수의 함수 T(n)을 구성하여, 데이터 수의 증가에 따른 연산횟수의 변화 정도를 판단
- 명령어의 실행시간은 컴퓨터의 하드웨어 또는 프로그래밍 언어에 따라 편차가 크게 달라지기 때문에 명령어의 실행 횟수만을 고려
- 알고리즘의 실행시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존하며,이 속도는 컴퓨터의 처리속도, 사용된 언어종류, 컴파일러의 속도에 달려있음
점근적 표기법(Asymptotic notation): 가장 큰 영향을 주는 항만 계산하고 중요하지 않는 상수와 계수들을 제거하여 알고리즘의 실행시간에서 중요한 성장률(입력값의 크기에 따른 함수의 증가량)에 집중- 최선의 경우(best case) :
오메가 표기법 (Big-Ω Notation)- 알고리즘 수행시 가장 비교연산 횟수가 적은 경우
- 어떠한 알고리즘이건
최선의 경우에는대부분 만족할 만한 결과를 보이기 때문에 알고리즘을 평가하는데 있어서 중요한 고려 대상이 아니다.
- 평균의 경우(average case) :
세타 표기법 (Big-θ Notation)- 알고리즘 수행시 가장 비교연산 횟수가 평균적인 경우
- 평균을 계산하기 위해서는 다양한 이론이 적용되어야 하고, 분석에 필요한 여러가지 시나리오와 데이터를 현실적이고 합리적으로 구성해야 하므로, 현실적으로 쉽지 않다.
- 최악의 경우(worst case) :
빅오 표기법 (Big-O Notation)- 알고리즘 수행시 가장 비교연산 횟수가 많은 경우
- 데이터의 수가 많아지면
최악의 경우에 수행하게 되는 연산의 횟수는 알고리즘 별로 큰 차이를 보인다. 따라서 알고리즘의 성능을 판단하는데 있어서 중요한 것은최악의 경우다.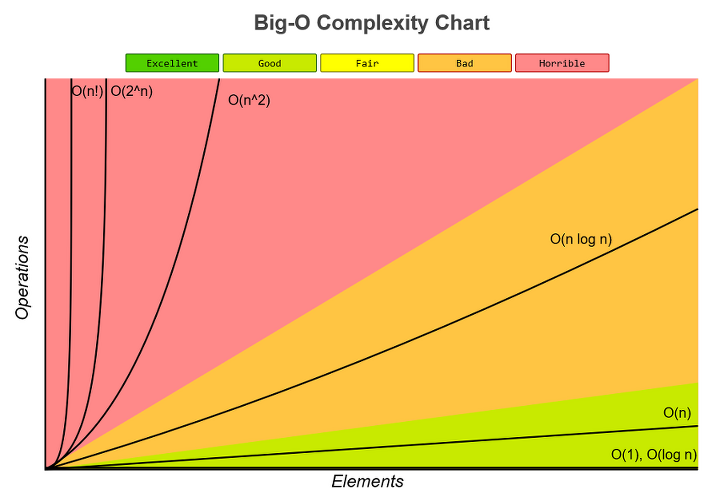
- 데이터 수의 증가에 따른 연산횟수의 증가 형태(패턴)을 나타내는 표기법
O(1): 상수형 빅-오. 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘O(logn): 로그형 빅-오. 데이터 수의 증가율에 비해서 연산횟수의 증가율이 훨씬 낮은 알고리즘O(n): 선형 빅-오. 데이터의 수와 연산횟수가 비례하는 알고리즘O(nlogn): 선형로그형 빅-오. 데이터의 수가 두 배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘O(n2): 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘.- 데이터의 양이 많은 경우 적용하기 부적절
- 이중으로 중첩된 반복문 내에서 알고리즘에 관련된 연산이 진행되는 경우 발생
O(2n): 지수형 빅-오.- 사용하기에 매우 무리가 있는 알고리즘
- 최선의 경우(best case) :
- 알고리즘의 수행
- 공간 복잡도(space complexity)
메모리 사용량에 대한 분석결과